论文阅读 Exploring the Performance Improvement of Tensor Processing Engines through Transformation in the Bit-weight Dimension of MACs
Exploring the Performance Improvement of Tensor Processing Engines through Transformation in the Bit-weight Dimension of MACs
Qizhe Wu1, Huawen Liang1, Yuchen Gui1, Zhichen Zeng1,3, Zerong He1, Linfeng Tao1, Xiaotian Wang1,2, Letian Zhao1 Zhaoxi Zeng1, Wei Yuan1, Wei Wu1 and Xi Jin1*
1 Department of Physics, University of Science and Technology of China, 2 Raytron Technology 3 Department of Electrical and Computer Engneering, University of Washington
TLDR: 现有GEMM计算架构主要集中于数据流或操作数重用,提出了systolic array等,但是这一考虑最小的粒度是单个乘累加单元。本文作者将GEMM与乘加器(MAC)本身设计相结合,最小单元变为移位/全加/半加/…等逻辑,比GEMM传统3层loop的场景下新增了更多的操作层级选择。综合考虑此类场景为Tensor Processing Engine提供了更大的优化空间,提供面积、时序、功耗的综合提升。(代码开源)
传统乘法器的设计
类似于竖式,通过位乘法+移位实现


常见的MAC计算原理和分析


基于MM的计算阵列架构:2Dmatrix, weight stationary / output stationary systolic array, 3D-Cube.
新颖的乘法器设计:array multipliers, Booth multipliers, Baugh multipliers, carry lookahead adders, carry select adders, carry save adders, Wallace tree, compressor tree.
MAC主要分为三个阶段(图2):1、编码被乘数生成部分积(PPs)2、压缩PP生成最终和和进位 3、全加器累加。
问题在MAC全加器高位宽累加内部的逻辑传播延迟(TPD)和面积成为瓶颈。Bucket Getter已经提出过图2G的方案,通过把浮点转换为定点加法减少了浮点累加器功耗,但没有解决高位宽累加的瓶颈问题。
研究人员提出了基于bit slice的方法替代MAC,比如Radix-2 bit-serial, Radix-2 bit-interleaved, higher width bit-slice , Radix-4 based slice.
以Radix-2 bit-serial为例(图2B)依赖于位本身的稀疏性跳过0元素、生成PPs、根据稀疏索引进行累加和移位。Radix-2 bit-interleaved同时处理多个数据(在多个数据相同的位权重部分做处理,无需移位操作)。Radix-2 based算法能保持位稀疏性,但需要很多的PPs累积。并且只能跳过0切片,不能根据1切片的稀疏性进行跳过。
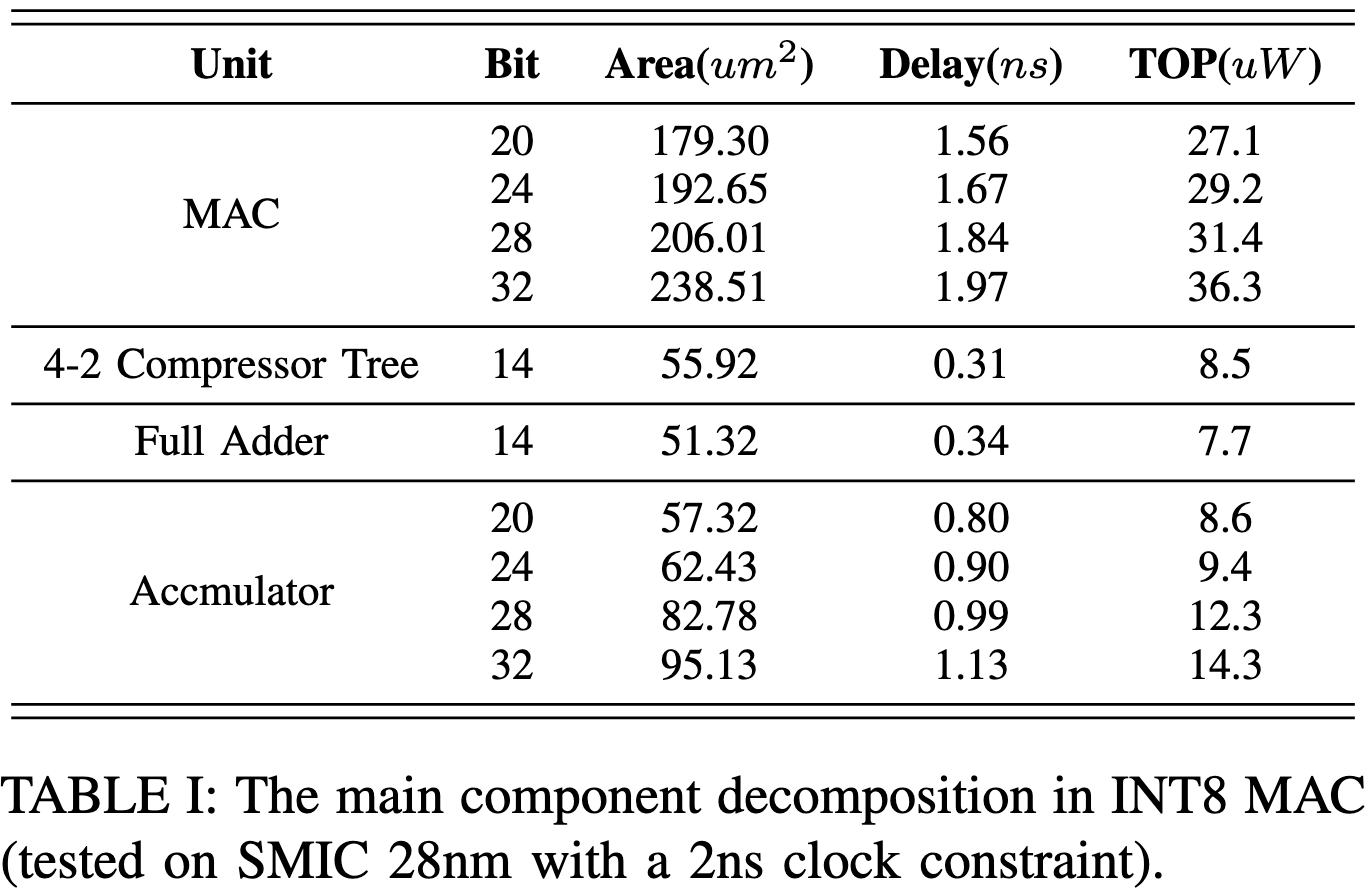
累加器的位宽在乘加器(MAC)中增加时,限制性能的主要因素逐渐转变为累加器的面积和延迟。
例如,在32位累加中,完全加法器和累加器所占的逻辑面积占61.4%,逻辑延迟高达74.6%,严重限制MAC频率。
以INT8为例,Radix4 parallel multipiler,n-bit乘数经过MBE/EN-T编码后能产生n/2 PPs。比如91,会产生编码数{1,2,-1,-1}和位权重{}.计算为91B=(B<<6)+(2B<<4)+(-B<<2)+(-B). PPs只需要计算+-2B, +-1B, 0即可,剩下的都是移位。然而不是所有的数字都会产生4个,有可能更少,更有利于计算速度和能耗缩减,比如124会产生{2, 0, -1, 0}。经过统计,在MBE编码下,68.4%会产生3个及以下的非0编码。在随机的矩阵测试中,1024*1024的矩阵平均产生了2.22个编码,但如果在纯GEMM场景中这种编码稀疏性会被隐藏,因此作者采用先encode,后sparse encode的两步方式来在后面一步中感知这种稀疏性,实现更高的能效。
本文提出的变换
本文新颖的地方在于,作者使用了新的MAC分析模型,将MAC中的硬件组件作为原语映射到loop中(如并行编码器、候选部分乘积生成器(CPPG)、部分积生成器、移位器、压缩器、全加器和高位宽累加器),挖掘隐含的并行维度。
本文根据分析(见下文)提出了图2A到2D到变换,MAC涉及到时间维度的累加,会造成高位宽累加的问题。但是可以在时间维度的累加结束之前使用Compressor来进行累加,在DFF内保留Sum和Carries。由于半加器延迟与操作数位宽无关,因此能减少将近一半的TPD。
对于bit slice稀疏计算的问题,本文还提出了图2B到2E的变换。将简单的跳过0单元转换为编码器+稀疏编码的组合。编码器使用修改后的Booth encoding(MBE)和EN-T encoding,和传统对于被乘数的稀疏编码不同,这里是对在经过编码器进行初步编码后的表示进行稀疏编码,再进行后续操作。图里面有一个例子,可以看到2B里面产生了4,4,5个PPs进行累加,但2E里面只需要进行3,2,2个PPs进行累加。
总结
本文贡献在于:1、新的notations,挖掘新的优化机会 2、提供了对比特稀疏加速器的系统分析,提出高频率低面积的bit serial方案恶化其他编码方法之间的比较。 3、四种细粒度优化方案,应用于经典的Tensor Process Engine (systolic array, 3D-Cube, multiplier-adder tree, 2D-Matrix)后,分别产生了**1.27×, 1.28×, 1.56×, 和 1.44×**的面积效率;**1.04×, 1.56×, 1.49×, 和 1.20×**的能源效率。若应用于比特稀疏加速中,比最先进的方案Laconic提高了12.1x的能源效率和2.85x的面积效率。
术语定义和示例描述见下文,主要是通过将运算顺序抽象为伪代码的方式实现形式化表达

由于本文要利用比特稀疏性,作者提出了一个新的隐含维度,即在乘法encode过后的位数BW和位权,如下对A进行拆分
$$C=A\times B=\sum_{bw=0}^{BW-1}SubA_{bw}\times B.$$
矩阵乘法可以根据这个被拆分为
$$C_{m,n}=\sum_{k=0}^{K-1}A_{m,k}B_{k,n}=\sum_{k=0}^{K-1}\sum_{bw=0}^{BW-1}SubA_{m,k,bw}B_{k,n}$$
下图A-E表示了在传统GEMM表示的基础上依次加入硬件感知带来的最终表示方案,A-B代表PE阵列在并行维度扩展,B-E按照作者提出的标记增加了乘法器和加法器具体的运算逻辑。
根据传统乘法器的运行逻辑,encode代表从原有的A中生成mux的选择信号。map代表根据B的值和对应位权生成的所有PPs,并根据encode结果选择输出的过程。shift代表根据位权进行移位。
由于累加是一个引入delay的关键因素,因此作者划分为更细粒度的half_reduce, add, accumulate进行精细化表示。
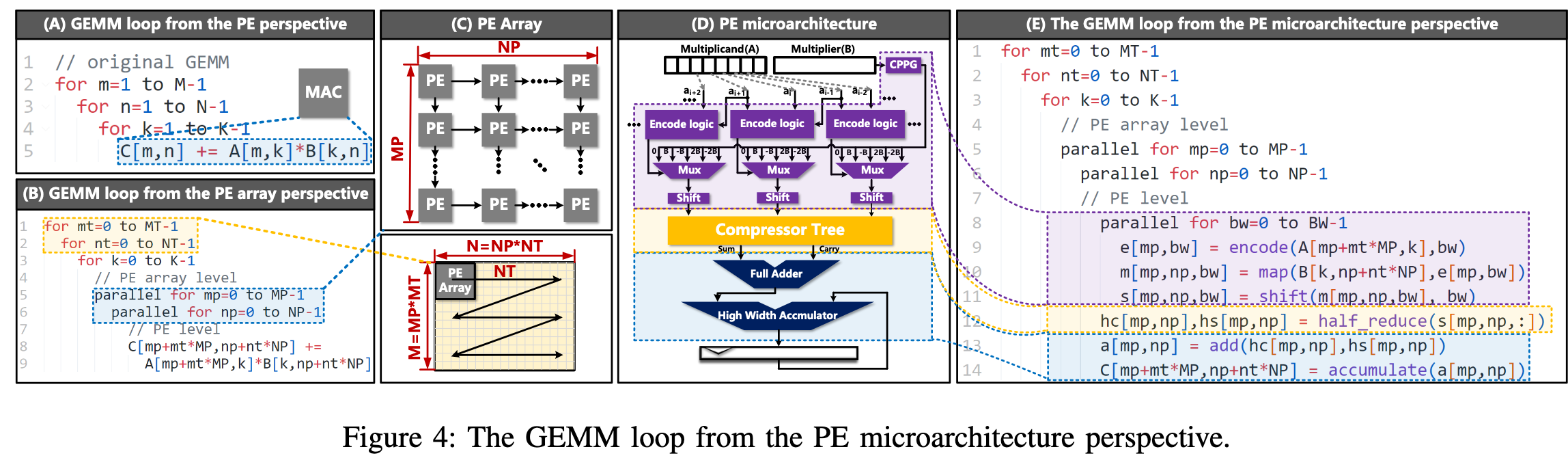
优化方案
Half Compress Accumulation Reduction (OPT1)

第一个优化首当其冲对大位宽累加下手。传统的eda工具需要保证乘法器的原子性一般按照A生成,即从compressor tree先经过full adder累加出一个最终值,再不断通过accumulator进行矩阵数值累加。
图A中,红色部分可以拆解为灰色的两个部分,即先将当前计算的compressor tree半加输出和之前结果(也存为半加)先累加,最后在全加。能够看到,“add”仅依赖于累积的acc c 和 acc s(A 第22行)。因此,“add”的结果在 K 维度的最后一次迭代之前并不需要,当 acc c 和 acc s 的累积尚未完成时,“add”的计算是多余的。
受到上述启发,有图B的改进。该策略在K维度的reduction中使用半加运算,确保逻辑延迟与累积位宽无关,从而减少对全加器和累加器的需求。减少了在同一K维度水平上合并acc s和acc c所需的“加法”操作。外部全加器可以单独用SIMD向量核心实现,以最终处理这些add,可以与GEMM阵列并行工作。并且由于SIMD向量核心每K个周期仅访问一次数据,因此完成这些任务所需的硬件资源也很少(假设有Mp*Np个运算阵列大小,只要Mp*Np/K个SIMD单元)。
结果:2ns约束下。关键路径延迟从1.95ns下降到0.92ns,并且延迟和位宽无关(没有进位链)。
Reduction under the Same Bit-weight (OPT2)


根据建模中有关GEMM的分析,我们可以很清楚的得到
$$C_{m,n}=\sum_{k=0}^{K-1}A_{m,k}B_{k,n}=\sum_{k=0}^{K-1}\sum_{bw=0}^{BW-1}SubA_{m,k,bw}B_{k,n}.$$
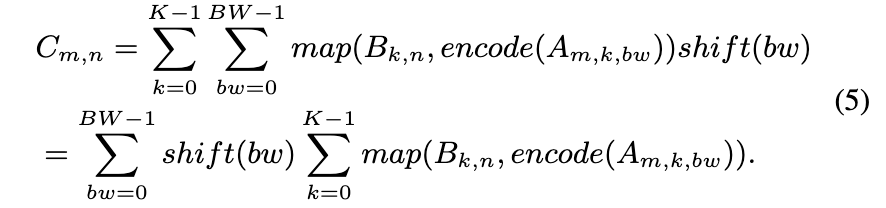
根据公式,“shift”仅仅和BW相关,可以提前。但是k维度是时间维度,如果要提前的话,意味着bw也会从空间维度变为时间维度,不然会出错。不过这种位置变换减少了移位器的数量,并降低了PE中后续组件(compress tree,DFF)的位宽,从而减少了面积。
作为一种折中,同时为了保持PE阵列的吞吐量,作者将维度K继续划分为kp和kt,kp为空间维度,能够填补由于bw变为时间维度后产生的bubble。第15行和第16行中的“half add”表示KP和KT维度的reduce逻辑。与在OPT1中类似,也可以将“移位”转移到SIMD向量核心,只需在KT维度完成减少后进行一次移位。在移位后,需要额外的全加器来减少移位的PP,以确保计算的正确性。这里使用简单的add而不是accumulate,SIMD核心的K个周期内没有和上一次结果的累加操作。这样进一步优化了SIMD部分,因为OPT1中simd需要在K的时间维度进行累积,现在的SIMD无需累积,仅需要add,可以铺开使用高性能流水线实现。
不过,这一改进有两个明显的缺点。第一个缺点是处理单元(PE)所需的带宽增加(kp维度的引入,B有更多的PPs)。第二个缺点是运算数B的CPPG逻辑和输入DFF数量增加,这将占用额外的面积,对于阵列设计,这些额外的面积可以在多个PE之间共享。这也是后续优化的起因。在考虑编码的稀疏性时,BW的时间展开是非常有利的。
Acceleration with the Sparsity of Encoding (OPT3)



这个优化解决了两个问题:OPT2中的带宽需求升级以及之前提到的利用比特稀疏性对计算进行优化。
为了描述修改后的架构,新引入了“sparse”和“sync”。“sparse”用于压缩输入并获取非零输入的索引。不同的是这里的“sparse”用于encode过后的数上,而之前的工作将其直接用于乘数。编码后的数字存储在PE的输入DFFs中(步骤❶),增加一个附加的sparse encoder输出编码数字的非零index,如步骤❷。该索引用作步骤❸中非零PPs和乘数B的选择信号。完成这个等效乘法根据sparse程度不同花费周期不同,在所有数字组合中平均2.2个时钟周期,可以接受。
同一列中的PE共享相同乘数A,因此它们在同一列中的计算时间是统一的,但在不同列之间可能会有所不同。因此引入“sync”以在PE列之间进行同步。如第六行,由于每一列变为异步了,可能出现bank conflict的情况,作者通过调整数据layout实现。假设原来A中在(M,K)位置编码,现在编码为(K1,MT,K2,MP),其中K1=MP,K2=K/MP。有相同K1的数字被存在一个bank里。两个bank之间的间距为dk(第12行)。B也类似,这样可以解决bank comflict。
(在K维度比较大时,各列之间的计算时延会收敛,证明详见原文)
总之,正如之前分析的,将sparse做用于encode之后的数上更有效,因为encode后的数直接影响PP的生成,并且允许跳过连续的1(之前的编码只能跳过连续0)。另外,也解决了OPT2带来的一些面积问题,在OPT2中,PE要并行计算所有PPs后选择,但OPT3中由于sparse加入变为串行(18行为时间维度),将原来的4-2 compressor变为3-2,减少了面积增长的问题。但没解决带宽需求增加的问题,因此作者提出了OPT4。
Extracted and Shared Encoder (OPT4C and OPT4E)



主要思想是重新排列 NP 和 KP 的顺序,并将“encode”和“sparse”环节移到 NP 维度的外层来节省编码环节的开销。由于操作数 A 是在PE 列广播的,每列中的 PE 可以共享相同的encoder和sparse encoder。
减少了每个PE中encode面积,降低了A的带宽需求。
将sparse encoder独立到PE阵列外,内存可以识别编码操作数A的稀疏性,并通过非零索引预取操作数B。使用平面外编码器,OPT2中的增加输入被分割并以顺序方式馈送给PE。每个PE仅访问一个共享的A编码及其对应的预取得到的B。PE仅包含一个CPPG、一个MUX和一个3-2 Compressor Tree,延迟仅为0.29ns。
为了进一步提升计算密度,作者还提出了一个OPT4E。将同一行中的4个PE安排成一个PE组(PEg),并且PEg共享一个Compressor Tree(四个3-2 Compressor Tree合并为一个共享的6-2 Compressor Tree)。此时,PE阵列的encoders,以及对应PEg中的CPPG,可以看作GEMM中的一个4输入部分和生成。提升大规模MM乘法操作效率,同时实现极低的延迟(作者称可轻松达到2GHz)。虽然和OPT4C比,逻辑延迟从0.29ns略微增加至0.40ns,但能够减少了PE阵列的面积和功耗(约3/4),提高了整体计算密度和能效。
实验
RTL + Design Compiler + SMIC 28nm-HKCP-RVT 0.72V
Innovus + VCS + PrimeTime功耗评估
时间余量8%~10%,int8 mul, int32 acc
单PE实验
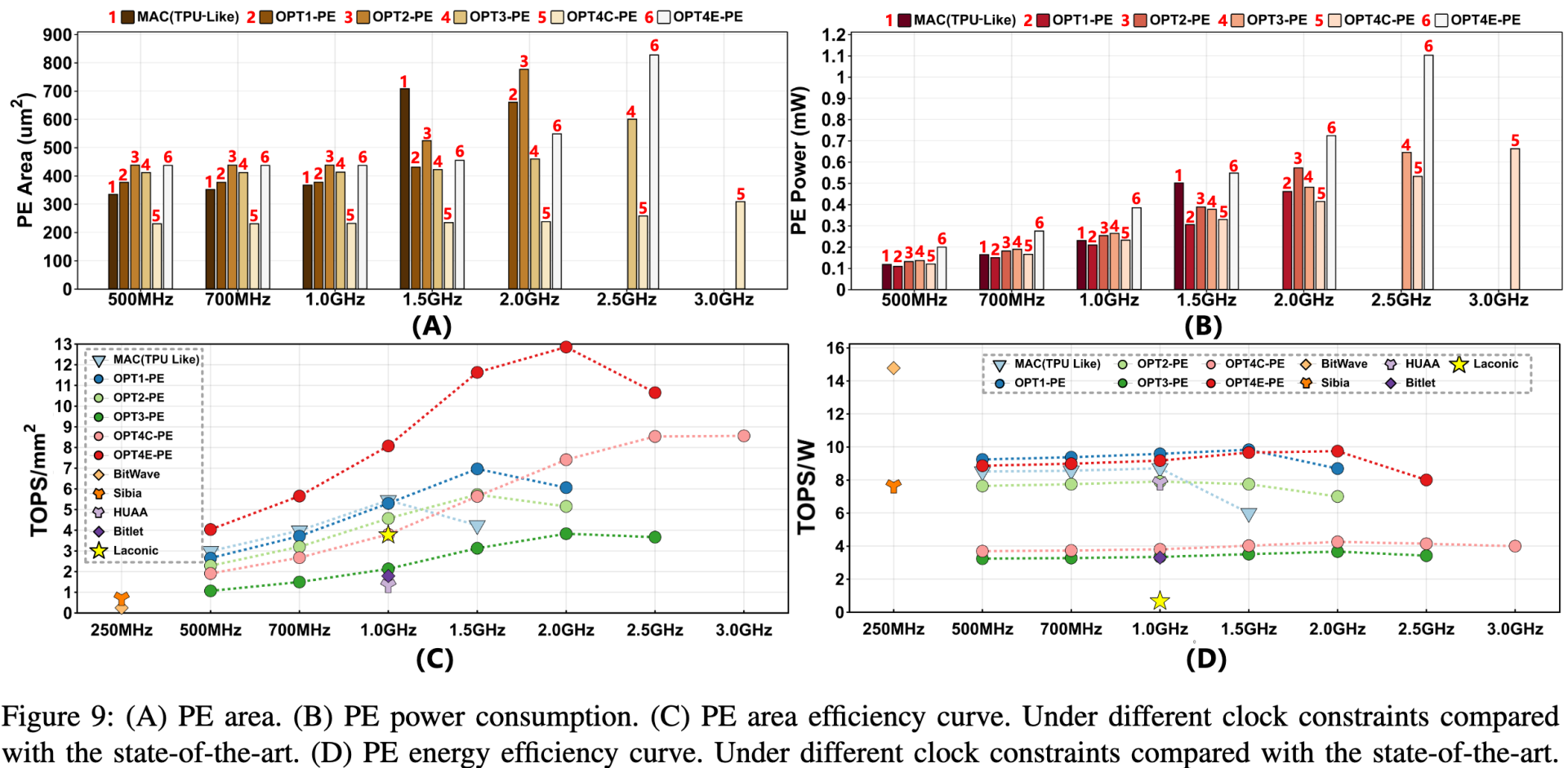
在28nm工艺下,达到1GHz代表了传统MAC(类似TPU)的性能拐点。然而,由于高位宽累加器的限制,当运行在1.5GHz时,传统MAC的面积显著增加(如图9(A)),从367um²增长到707um²。
对于传统MAC而言,超过1GHz并不会导致面积效率的进一步改善(如图9(C)倒三角)。
OPT1 ∼ OPT4中,延迟与位宽无关。因此可以在超过1.5GHz的频率下运行,并实现高面积效率(9C)。
1.0 GHz到1.5 GHz之间,OPT1的合成面积仅增加了1.14倍,而TPU则增加了1.93倍。这代表了在1.5GHz下OPT1的面积效率有了显著改善。
OPT2减少了reduce逻辑和输出DFF的面积,但PE带宽占用更大,面积和功耗增加。因此并没有在单个PE有明显优势。
OPT3 利用系数性跳过PP为0的计算,组合逻辑的面积和延迟显著降低。1.5 GHz ~2.0 GHz 时,OPT3 的面积仅增加 1.09 倍,峰值频率达到了 2.5 GHz,面积效率性能拐点在 2.0GHz 以上(与 Laconic 相当,Bitlet 的 2.12 倍,Sibia 的 5.28 倍,Bitwave 的 15.2 倍)。但用于比较的架构的时钟频率都仅有250MHz~1GHz。这些架构瓶颈主要体现在reduce环节,限制了峰值频率(类似于 MAC,1GHz)。
OPT4C 和 OPT4E通过在 PE 列之间共享编码器,使 PE 更加轻量,并通过sparse encode预取操作减少input DFF面积。相比OPT3 面积效率更好。OPT4E 进一步平衡了DFF和逻辑电路之间的面积比,以实现面积效率。
能耗方面,通过最小化逻辑设计中的寄存器宽度来降低高频下的功耗。如OPT4C和OPT4E的设计中减少了输入和输出DFF的需求,同时平衡了逻辑面积和DFF面积。OPT4E表现最好,在保持能源效率的同时实现了显著的计算密度。
PE阵列对比
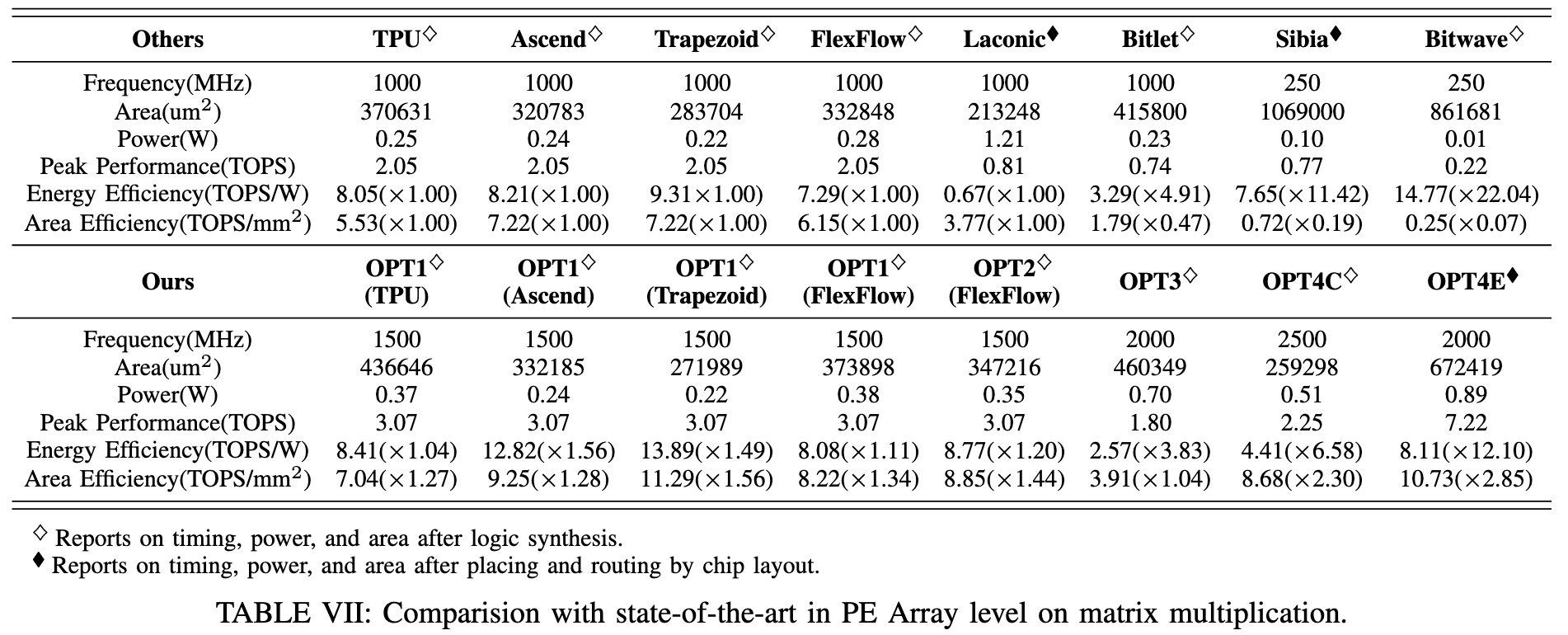
对象:TPU (systolic array), Ascend (3D-Cube), Trapezoid (multiplier-adder tree), FlexFlow (2D-Matrix)
由于只有OPT1/2是在传统阵列上进行的改进,因此在这些架构上的优化都只到OPT1/2
在所有设计上都有面积效率优势(1.27, 1.28, 1.58, 1.34倍)和能源优势(1.04, 1.56, 1.49, 1.11倍)
和其他基于bit-slice技术的array对比,通常这些方法通常显著提高能效,但在面积效率上一般较差。OPT4E 不仅保持了良好的能量效率,还显著增强了位切片架构的计算密度。
LLM/DNN负载下的测试




OPT4E提供的吞吐量与受乘数编码后PP的数量和向量的K维度大小有关。
如图A所示,传统MAC总是并行reduce 4个部分积,导致计算能力和能耗保持不变(黑色)。
OPT4C中单个PE的面积(81.27um²)约为并行MAC(246um²)的三分之一。
在最佳情况下,所有输入在编码后仅产生一个部分积,实现了常规MAC吞吐量的两倍,同时节省了三分之一的能量。
在最坏情况下,所有输入在编码后产生4个部分积,其计算能力相当于常规MAC的一半。
在更一般的情况下,对于一组正态分布的向量,MBE和EN-T编码的部分积平均数量分别为2.41和2.22。因此,单个OPT4C可以实现接近(1.8 GOPS)的吞吐量,接近常规MAC,同时具有更低的能耗。
作为同面积下的比较,三个OPT4C和一个OPT4E和一个MAC面积相似,但吞吐提升2.7/3.6x,并且能耗更低。最坏情况下,仍然可以实现加速。
由于OPT4E需要各维度之间的sync,因此最终结果还和需要reduction的大小有关。更高的向量维度能够使每列计算时间趋向一致(论文中有证明)。以GPT-2的Transformer层和MobileNet的DWC-PWC为例(图11~图12)采用一个脉动阵列和相同面积的OPT4E比较推理延迟。我们记录计算最快的列(Busy-Min PEs)、计算最慢的列(Busy-Max PEs)以及平均Busy比例(Busy-Average PE)。在GPT-2的MHA中,高维矩阵乘法导致空闲时间很少(几乎都同时完成)。MobileNetV3在DWC的累加维度比较低,而在PW层的维度高,导致DW层的利用率低于PW层。
在其他端到端的比较中(图12,13),MobileVIT、VIT和GPT-2的加速比最高,性能分别提高了1.89倍、2.02倍和2.16倍。具有更高累加维的网络能源效率也更高。